Наибольшее и наименьшее значение функций (профильный уровень, 12)

Сегодня научимся находить наибольшее и наименьшее значение функции, а также точки min и max.

Общая методика решения задач на исследование функций выглядит следующим образом:

1. Находим производную функции по таблице производных:

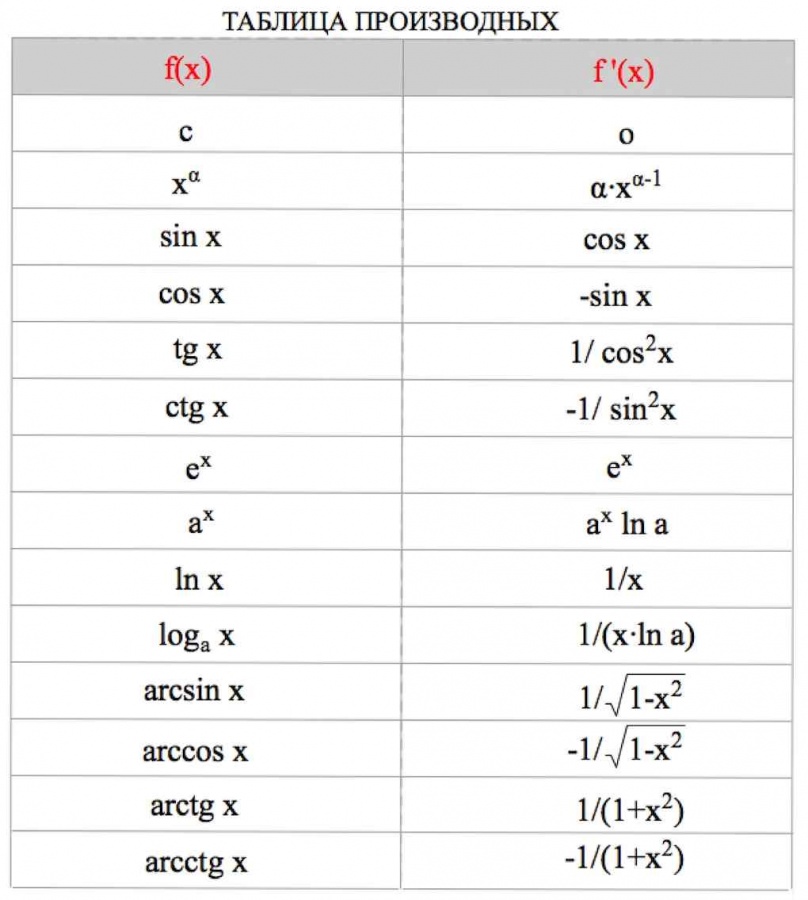
Ресурс: egemaximum.ru

При этом учитывая вид выражения:

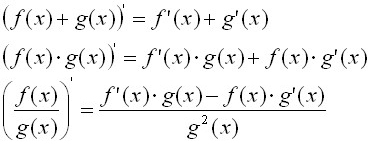
Ресурс: otvet.imgsmail.ru

2. Приравниваем производную функции к нулю, т.к. нам нужны экстремальные точки, а в них производная функции равна нулю.

Ресурс: cos-cos.ru

3. Отбираем из полученных значений х, те которые соответствуют точкам max/min, учитывая взаимосвязь функции с ее производной (если производная больше нуля, то функция возрастает, меньше нуля – функция убывает), т.к. геометрический смысл производной – это угловой коэффициент касательной.

4. Если необходимо найти наибольшее/наименьшее значение функции, берем точки max/min и вычисляем значения функций в этих точкак – это и будет наибольшим/наименьшим значением функции. Если есть ограничения на отрезке [a,b], то считаем значение функции еще и в них и из полученных выбираем наибольшее/наименьшее.

Задача.

Источник: сайт решу ЕГЭ.

Найдите точку максимума функции

\[ \begin{equation*}  у=x^3-48х+17  \end{equation*} \]

Решение.

Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Ответ: -4.

Записаться на пробный урок в MathClub по скайпу: