Нестандартные задачи

Рассмотрим серию нестандартных задач. Их отличает то, что они используют смешанные методы, а также нетиповой способ решения.
Задача 1
В прямоугольный треугольник с катетами 12 и 5 вписываются всевозможные прямоугольные треугольники так, что их катеты параллельны катетам исходного треугольника, а вершины лежат на разных его сторонах (не вершинах). Найдите наименьшее значение длин гипотенуз вписанных треугольников.
Решение
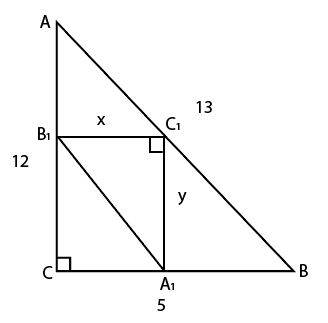
\[ \Delta AB_1C_1 подобен \Delta ABC \]
\[ {х\over{5}}={12-y\over{12}} \]
\[ y=12-24x \]
\[ A_1B_1=\sqrt{x^2+y^2} \]
Задача сводится к поиску наименьшего значения функции:
\[ f(x)=x^2+(12-24x)^2=6,76x^2-57,6x+144 \]
Ответ: 4,26
Задача 2
Найдите наибольшее значение n при котором утроенное количество всех n-значных натуральных чисел, содержащих цифру 0 (в своей десятичной записи), меньше удвоенного количества всех n-значных чисел, не содержащих цифру 0.
Решение
n-значных чисел – 9*10^(n-1)
не содержащих нуль – 9^n
содержащих нуль – 9*10^(n-1)-9^n.
Найдите наибольшее n, при котором
\[ 3*(9*10^{(n-1)}-9^n)<2*9^n \]
\[ 27*10^{(n-1)}<5*9^n /:9 \]
\[ 3*10^{(n-1)}<5*9^n /:(10^{(n-1)}*5) \]
\[ 3/5<(9/10)^{(n-1)} \]
\[ 0,6<(0,9)^{(n-1)} \]
\[ 0,6<(0,9)^4=0,6561, но 0,6>(0,9)^5=0,59049 \]
Поэтому наибольшее n=5.
Ответ: 5.
Задача 3
Решить неравенство
\[ {x^4-x^2-2x-1\over{x^2-(2-\sqrt7)x-2\sqrt7}}\leq0 \]
Решение
\[ {x^4-(x-1)^2\over{x^2-2x+\sqrt7x-2\sqrt7}}\leq0 \]
\[ {(x^2-x-1)(x^2+x+1)\over{x(x-2)+\sqrt7(x-2)}}\leq0 \]
\[ {(x^2-x-1)(x^2+x+1)\over{(x-2)(x+\sqrt7)}}\leq0 \]
Ответ: 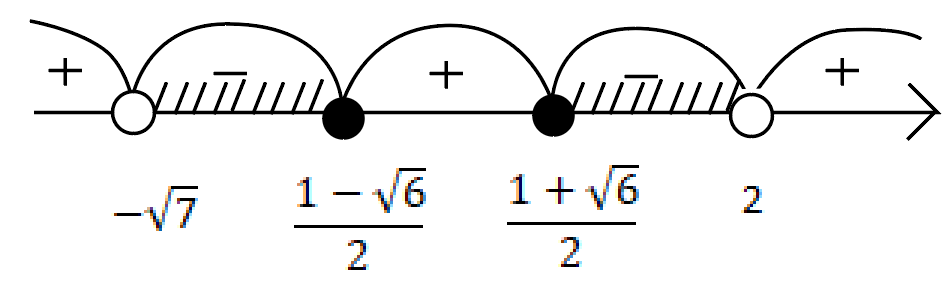
Задача 4
Решить уравнение
\[ 4x^2+12x+11+\sqrt{(-3x-2)}={{3x+1}\over{x+1}} \]
Решение
\[ 4x^2+12x+11+\sqrt{(-3x-2)}={{3x+1}\over{x+1}} \]
\[ (2x+3)^3+2+\sqrt{(-3x-2)}=3-{{2}\over{x+1}} \]
\[ ОДЗ: (-{\infty};-1)\cup(-1;-2/3] \]
1)
\[ на (-{\infty};-1,5] \]
левая часть функции убывает, правая часть возрастает, следовательно по теореме о монотонности функции на этом промежутке не более одного корня. Поэтому x=-2 – единственный корень.
2) на (-1,5;-1)
\[ (2x+3)^2 \]
\[ \sqrt{(-3x-2)} \]
Левая часть меньше 5.
Правая часть
\[ 3-{{2}\over{x+1}}>7 \]
нет корней.
3) на (-1;-2/3]
левая часть больше нуля
\[ 0<x+1<1/3 \]
\[ {{2}\over{x+1}}>6 \]
\[ 3-{{2}\over{x+1}} \]
нет корней.
Ответ: -2.
Решала: Елена Шарич

