Геометрические задачи с4 ЕГЭ (профиль)

В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) докажите, что биссектриса угла С делит отрезок МN пополам
б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Решение.
а) Обозначим K точку пересечения отрезков AM и BN. Треугольник ABN равнобедренный, так как в нем AK является биссектрисой и высотой. Следовательно, AK является и медианой, то есть K — середина BN. Получаем, что AN = AB = 6, откуда NC = AC − AN = 3.
Рассмотрим треугольник ABC, биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам: BM : MC = AB : AC, учитывая, что длина BC равна 5, получаем: BM = 2; MC = 3.
В треугольнике MNC стороны NC и MC равны, следовательно, треугольник MNC — равнобедренный, с основанием MN. Значит, биссектриса угла C также является медианой и высотой. Таким образом, получаем, что биссектриса угла С делит отрезок MN пополам.
б) Рассмотрим треугольник PMN: отрезок PO перпендикулярен прямой MN и делит её пополам, следовательно, треугольник PMN — равнобедренный с основанием MN. Значит, PM = PN и отношение AP : PN = AP : PM.
В треугольнике AMC отрезок CP — биссектриса, поэтому AP : PM = AC : MC = 3 : 1.
Ответ: 3 : 1.
Задача 2
Окружность с центром O проходит через вершины B и C большей боковой стороны прямоугольной трапеции ABCD и касается боковой стороны AD в точке T. Точка O лежит внутри трапеции ABCD.
а) Докажите, что угол BOC вдвое больше угла BTC.
б) Найдите расстояние от точки T до прямой BC, если основания трапеции AB и CD равны 4 и 9 соответственно.
Решение

а) Угол BTC вписан в окружность, а угол BOC — центральный угол, опирающийся на ту же дугу. Следовательно, ∠BOC = 2∠BTC, ч.т.д.
б) Из условия касания окружности и стороны AD следует, что прямые OT и ADперпендикулярны. Пусть окружность вторично пересекает прямую AB в точке L и сторону CD — в точке M. Тогда диаметр окружности, перпендикулярный стороне AB, делит каждую из хорд BL и CM пополам. Обозначим OT = r, тогда
По теореме Пифагора По теореме о касательной и секущей
Следовательно,
Аналогично
Из теоремы синусов следует, что BC = 2r · sin ∠BTC. Пусть h — искомое
расстояние от точки T до прямой BC . Выразим площадь треугольника BTC двумя способами:
Отсюда получаем, что Следовательно,
Ответ: 6.
Задача 3
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что ∠AHB1 = ∠ACB.
б) Найдите BC, если и ∠BAC = 60°.
Решение
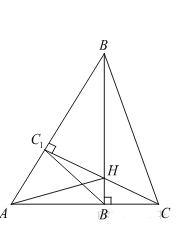
а)
Треугольники ВА1Н и ВСВ1 подобны (по двум углам). Т.к. углы НА1В и ВВ1С — прямые, а угол В общий. Следовательно углы В1СВ и ВНА1 равны.
Углы АНВ1 и ВНА1 равны как вертикальные. Следовательно, АНВ1=АСВ.
b) Треугольники ВА1Н и ВСВ1 подобны по доказанному, поэтому ВС=kАН и ВВ1=АВ1.
Т.к. угол ВАА1=60 градусов, то угол АВВ1=30 градусов, следовательно 2АВ1=АВ=2х.
По теореме Пифагора
\[ ВВ_1=\sqrt3x \]
Следовательно
\[ k=\sqrt3 \]
Отсюда ВС=24.
Ответ: 24.

